https://pruning101.com/?p=2873

の日本語版

特長とメリット

 おさらい　アルキメデスの原理

”　浮力の大きさは物体が排除した流体（水）の重さに等しい。”

図１において、浮力＞重力ならば、物体は上昇を続ける。やがて、物体は水面の上に現れる。　

水中に比べて、排除する水量は減る。　

結果、浮力も減る。　どこかで浮力＝重力となる水深がある。

このバランス水深を喫水線という。

 

なお、浮力自体も、もとはといえば、重力に起因する。

よって、喫水線より下の水中において浮力は水深と関係なく一定である。

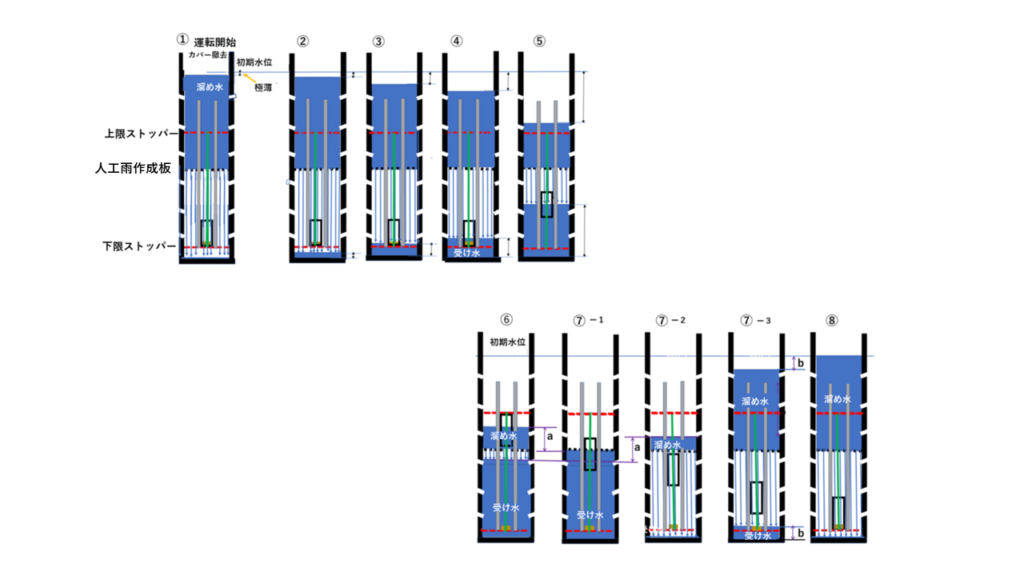
運転前準備

　

物体の繰り返し上下運動

予備ノート

時系列（図３、図４）の各ステージを説明する前に、全体を通していくつかの重要な点。

１サイクル　(①②…⑧）の各ステージの説明

エネルギーと電力

物体は、　上限ストッパーと下限ストッパーの間を繰り返し上下運動（図２、図３）。　この力学エネルギーを電気として取り出すことが最終目的。　

 このため、機械エネルギーから電気エネルギーへの変換を考える必要がある。

このため、機械エネルギーから電気エネルギーへの変換を考える必要がある。

たとえば、クランクシャフトから発電機に繋げる。　この標準的な手法の替わりに、図のような方法も考えられる。　これは、電磁誘導の原理に基づくものであり、エネルギーのロスが小さいことが期待されるpruning101.com/?p=2829。

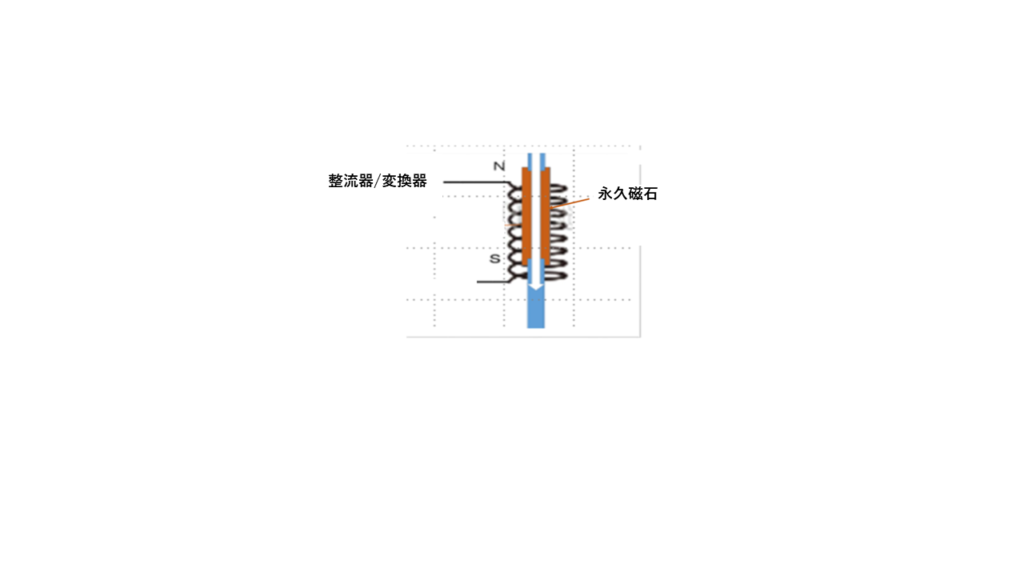
物体が最高位置の上限ストッパーに達したとき、物体が持つ位置エネルギー　

（ポテンシャル・エネルギー）は、下限ストッパーの位置を基準にして、

 Ｕ＝Ｍｄ　　　　　[ kg·m²·s⁻²　, ジュール]　　　　　　　　　　　式１

ここで、　Mは物体の質量　[ｋg]、d は上限ストッパーと下限ストッパーの間の距離[m]。

Uは装置が１サイクル間に行った仕事（物理量）　に相当する。

電力にも関係する仕事率、パワーP　とは、この仕事を成し遂げた時間が関係する。　時間が短ければ短いほど大きなパワーとなる。　

そこで、１サイクルに要す時間をT秒とすれば、本装置のパワーは

P＝U/T となる。

そこでTを以下で見積もってみる　。

物体の運動環境は二つに分かれる（図３、図４）。

すなわち、

A　　浮力環境

　物体は全体　または１部　が水で覆われ、浮力が働く。

B　　シャワー環境

浮力はゼロ、空気抵抗を無視して、物体は重力による自由落下。

  

図３と図４を俯瞰すると、AとB　は概ね半々。　そこで、　AとBで費やす時間を別々に考える。　そして、その際、物体は上限ストッパーと下限ストッパーの間を

動くものと仮定する。　すなわち, この移動距離はd　となる。　その上で、AとBで費やす時間の平均を求める。

 

実施例  

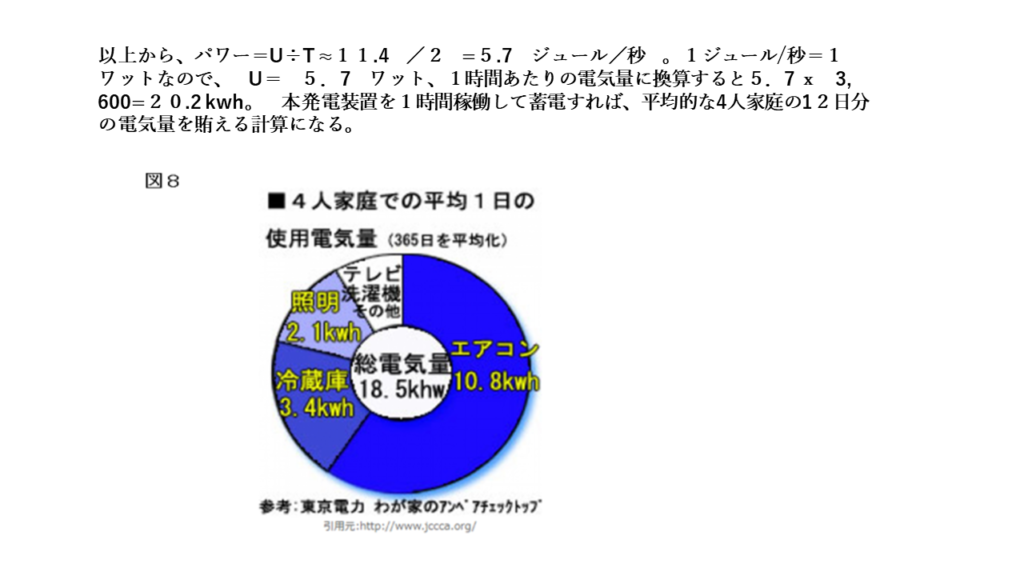
実施例　１

 

 

実施例２

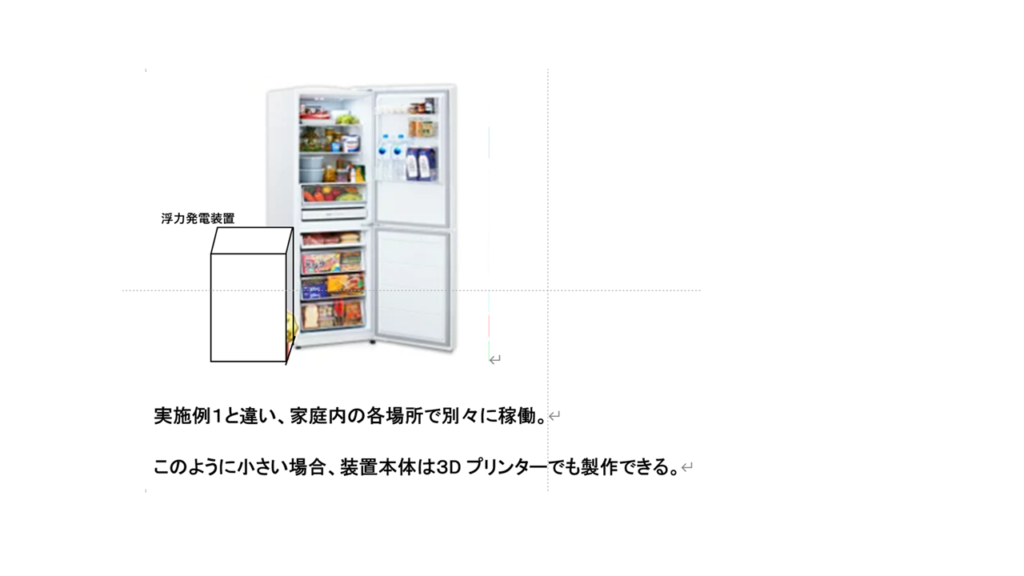
実施例３

あとがき