Major Characteristics and Merits

Introductory Review: 

  Archimedes’ Principle

Ｔhe loss in measured weight of an object  immersed in a  fluid is equal to the weight of the displaced fluid.

As illustrated by Ｆig.1, as far as buoyancy> weight　holds， the object keeps rising  in water. Eventually, the object emerges from the water surface.  And the water volume displaced by the object decreases. As a result, buoyancy decreases.  During this development, there exists a water depth where balancing occurs , namely,  buoyancy=weight. This is referred to as water line. 

 Afterall, buoyancy is attributed to the terrestrial gravity.  Thus, below the  water line, buoyancy  does  not change regardless of the water depth. 

Pre-Operation Framework

 

 

 

Preliminary Notes

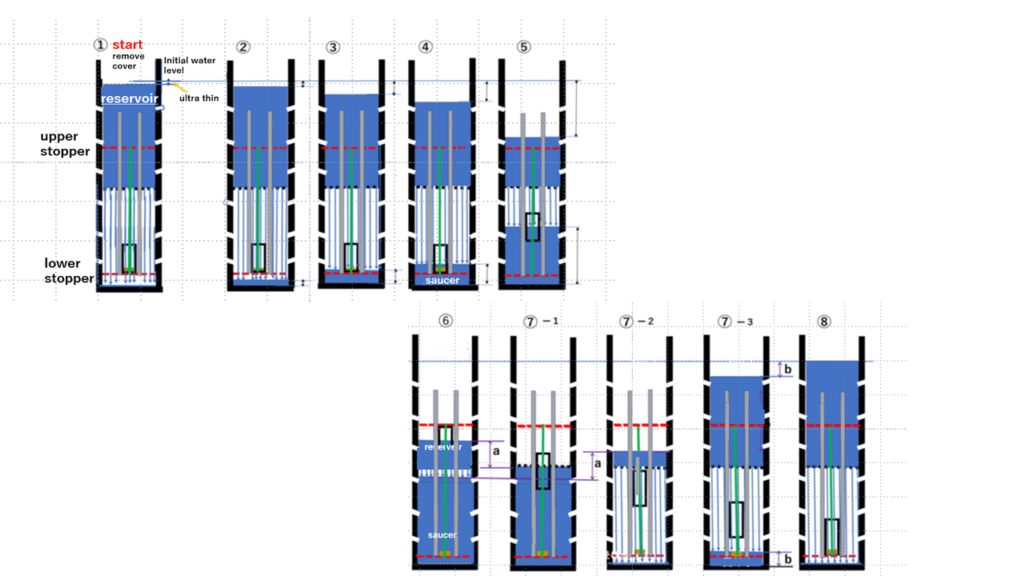
Before  explanations of cyclic time series  ①～⑧, there are some points important throughout.

 　Explanation of  one -cycle time series ①②③…⑧

 

 

 

 

 

 

 

 

Electric Power Evaluation

 The object repeats up-down motion between upper and lower limit stoppers.  It is the ultimate goal to　acquire electricity out of the mechanical up-down movements.

As for the mechanical-to-electrical energy conversion, a dynamo connected to a crank shaft m isay be considered. Instead of such conventional method, one may think about alternative approach based on electromagnetic  induction illustrated below (pruning101.com/?p=2829). This is a prospect since energy loss is expected to be small. Further research   remains to be made in this regard.  

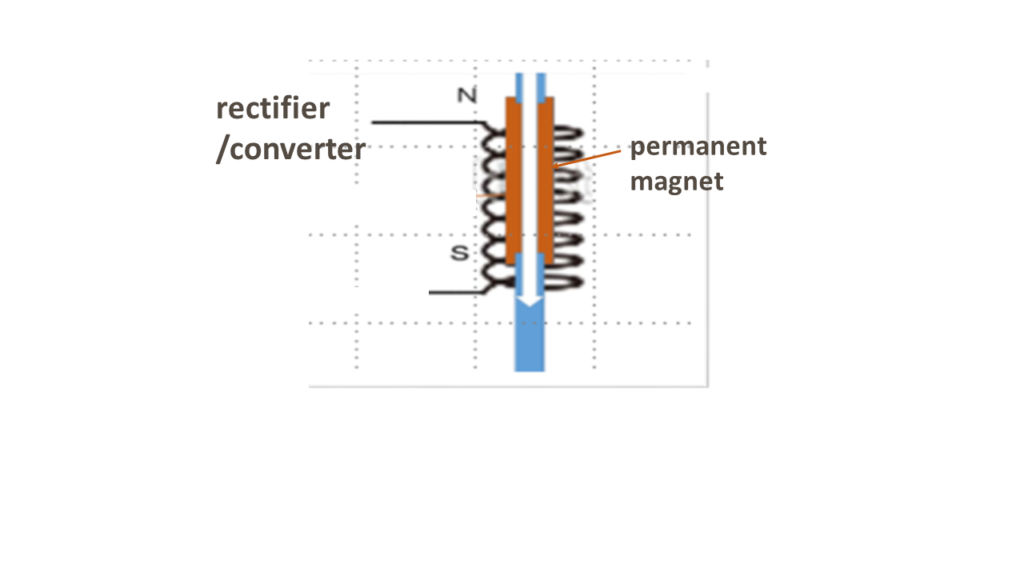
 When the object arrives at the upper-limit stopper position, the object has potential energy U （the lower-limit position is the base）.

Thus,

 Ｕ＝Ｍｄ　　　　　[ kg·m²·s⁻²　, Joule]　　                Eq.1

Here, M  [kg]  is mass of the object  , d [m]   is distance between upper　and lower limit  stoppers.  U corresponds to the work (term of physics) done by the object during  one up-down stroke.

Electric power is related to the time spent to attain the work mentioned above. That is to say, the shorter the time, the larger the electric power.  Thus, if T [sec] denotes the time, the electric power P [Joule/sec=watt], is expressed as follows.

P＝U　/　T

 

Now, T is estimated as follows.

Regarding the motion environments of the object, two types A and B are recognized,

A     Buoyancy environment

     The whole or a part of the object is surrounded by water, so that buoyancy works.  

B     Rain (shower) environment

      There is no buoyancy.  Basically ( aerodynamic resistance is negligible), The object motion is   gravitational free fall.  

 

Overlook view of Fig3 and Fig4 tells that A and B are roughly half-and-half during a single cycle. So, estimation of T in question is considered separately. And, it is assumed that the object moves between the upper and lower limit stoppers.

Then, the average of T of A and T of B will be calculated. This result is thought to be an approximation of the time spent for one cycle.

A     Buoyancy environment

Let us denote entities relevant to the object as follows.

 M: mass  [kg]  W:  weight:  [kg m sec-2 ] α: acceleration  [m sec-2] F: buoyancy  [kg m sec-2 ]

 Newton’s law of motion says mass x acceleration = force.  Accordingly,

Mα＝F-W 

 Since W=Mg  (where g stands for the gravity acceleration constant), the forgoing equation leads to

  α=  (F/W-1)g                   Eq. 2　

A problem is how large buoyancy should be in comparison to the weight W.

For example, if F>=2W (buoyancy is twice greater than weight) , then  α　> = g. This means that the object in water would move upward with a speed much faster than free fall. This is not realistic for hydrodynamic reasons. That is, high speed not only increases water resistance, but also induces turbulence and eddy.

Such  troublesome flows would invite instability of the object’ movements, and in the first place, there is no guarantee that Archimedes’ principle will work.

   .

So, for the condition F>W to be moderate,

F=1.1  W         Eq. 3

.is set for the rest of present analysis.  Then, from Eq.2 , upward acceleration is  

α＝0. 1g .       Eq. 4

This is 10% of the free fall acceleration and is thought to cause no hydrodynamic problem.     

In general, distance=acceleration x time² /2.

In the present case, distance is between upper and lower limit stoppers、thus

distance=d [m]．Thereby, d=αT²/2 , and  

Since α＝0. 1g from Eq. 4,   

   T= Eq.5

B   Rain environment

 There is no buoyancy. Acceleration α is downward with gravitational constant g, ie α=g. Thus, the time for the object to spend from the upper to bottom limit stopper is

     T=                           Eq.6.

  As mentioned before, for the present approximation analysis, T  to complete one cycle  is average of T of Eq. 5  and T of Eq.6.

Accordingly, by using Eq.1 the electric power is estimated as follows.

 

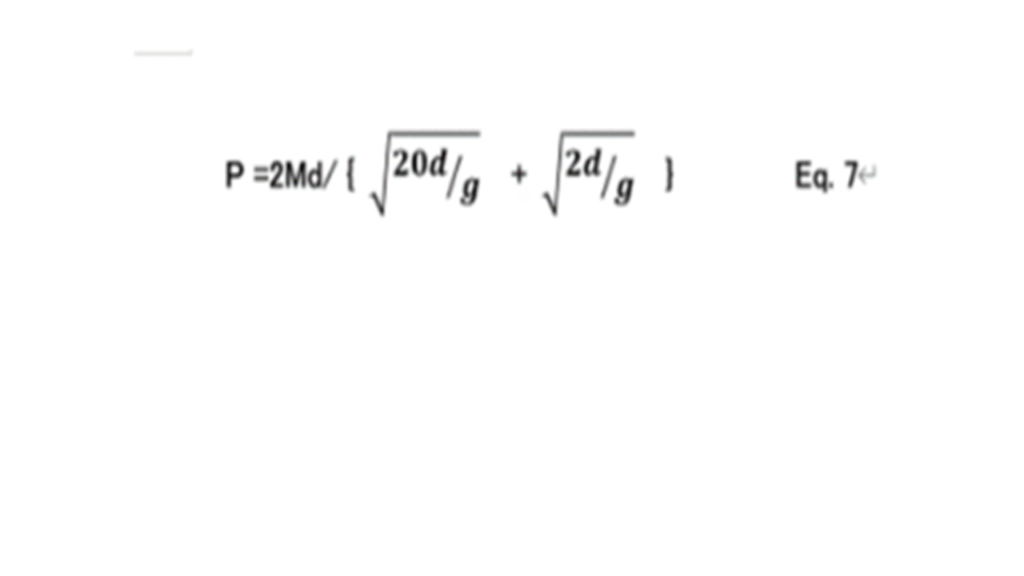
Implementation Example 1 

Home power supply site for everybody of a family— illumination, air conditioner,

refrigerator, washing machine, television sets, computers, etc

 

The object itself (the hollow part)  is a cube of 50 cm x 50cm x 50 cm[liter]. Since the specific gravity of water is 1, the mass M= 125 [kg]

The distance d between the upper and lower limit stopper is 1 [m].

As for the object’s weight W，W is adjusted such that F=1.1 W for stability reasons discussed earlier. This adjustment is made appropriately by choosing materials and thick ness of the framework and walls. 

Next, the time T for the object to spend one cycle is estimated.

For the buoyancy environment A (upward movements), the time is 1.43 sec from Eq. 5.　For the rain environment B (downward movement), the time is 0.43 sec from Eq.6.　Thus, using Eq. 7,

T= ( 1.43 + 0.45 )/2=0.94 sec.

In practice, however, the time will be somewhat longer than this, due to hydrodynamic drag and friction as well as air resistance.  Accordingly,

T=2 sec

is assumed here. This is thought a moderate setting from stand point of the power generating performance.

Now, since M=125 [kg] and m=1 [m], potential energy U that the object possesses at the upper limit stopper position is

  .U=Md=125 [ Joule]  and the electric power is P= U/T= 62.5  2 [Joule sec ^-1 = watt ].  Thus, electrical quantity gained by 1 hour operation is 62.5 x 3,600 =225kwh. If this electricity is accumulated by storage battery, average electricity needed by four – people family is covered for 12 days.

Average electric quantity par day used by four-people family

air conditioner                        10.8 kwh

refrigerator 　　　　　　　　　　　　　 3.4 kwh

illumination　　　　　　　　　　　　　  2.1 kwh　

washing machine,　television sets, etc.　

Total                              18.5 kwh

Implementation Example 2

The water tank is 30 m high, the cross-sectional area is 6 x 6=36 m².   The object is a hollow cub of  2 x 2 x 2 = 8 m³ .  Volume of the replaced water is 2 x 2 x 2 = 8 x 100³ cm³ = 8,000 [liter].  So, M=8,000 [kg] =8 [ton].   The distance d between upper and lower limit stoppers is 15 [m].  Time T is , ５．５　sec for the upward motion (Eq. 5), and 1.7 sec for the downward  motion (Eq. 6).

T for  one cycle is estimated  from Eq.7.  as follows.　

T = (5.5 + 1.7)/2 = 3.6 sec.

On the other hand, when the object is at its highest position, the potential energy is U=8000 kg x 15 m =120,000 [ Joule]. Thus, the power is

P = 120000/3.6=33000 [Joule　sec^-1 ].

Accordingly, the electric quantity par hour is about 200 kwh.

Implementation Example ３

Unlike Implementation　Example 1,　this is a cocept that aimes at intra-house 

individual rooms.

For small implementations like this, the present Archimedean device can be fabricated by using a 3D printer.

 

Closing Notes

In case of hydraulic power generation, water falls from a high site such as dam, and forms rivers’ water, and ultimately the water is released to the sea.

If the sea temperature is high there, water vapor is created.  And the vapor is diffused into the sky with   ascending air current. Then, rain clouds are formed for rain to fall. 　This way,　endless circulation of water is acomplished  by nature.  Namely

high↓low , low↑high 、high↓low , low↑high,・・・・

An analogy may be recognized from correspondences such as

 rain ⇔ shower    dam ⇔ reservoir    sea ⇔ saucer ascending air vapor ⇔ buoyancy

Water plays the leading role for both conventional hydro-electric and the present Archimedean methods.  Like here, the hydro-electric power stations  work also irrespective of night and day.  However, such stations  depend on  weather conditions.

Moreover, wheras  various  environmental protection issues always exist, the present Archimedean method affects very little natural, social and economic environments.

Finally, constraction/meintenance cost is low in  parison to other kinds of plant of similar performance for electric power generation.   This point seems worthy to consider when construction of new plants or re-operation of old plants (eg., nuclear power station) are being planned.