＜特長＞

一定量の水があれば機能する発電。
水の出し入れ用の開閉（例、電磁バルブ）は一切不要。

太陽光も風力も不要。　化石燃料もバイオ燃料も核燃料も不要。
天候や昼夜に関係なく、地球上の何処でも運転可能　温室効果ガス排出ゼロ。

説明の前に、浮力に関係する基礎事項のおさらい。

 ●アルキメデスの原理

浮力の大きさは、物体が排除した流体の重さに等しい

●浮力、重力、喫水線

 

 

図２において、物体が排除した水の体積はＣ＝Ｄ＝Ｅ＞Ｂ＞Ａ、よって、浮力の大きさも　Ｃ＝Ｄ＝Ｅ＞Ｂ＞Ａ。

 物体の重量をＷとすると、浮力（上向き：＋）と重力（下向き：＋）の合力は　合力＝浮力―重力。よって、物体は、浮力＞重力ならば上昇、浮力＜重力ならば沈下。浮力＝重力のとき、上下方向に静止。　

静止は、通常、物体の上部が水面上に顔を出している場合（Ａ，Ｂ）。　このとき、物体と水を区分けする境界を喫水線という。

 本装置に固有な「法則」

 冒頭イラスト①、②、③　のどのステージに於いても、装置全体の中にある水量は不変・一定。 このことは、シャワーの水が主役である④、⑤、⑥のケースでも然りです

 .

 

装置の説明　冒頭イラスト①、②、③

 

①は、運転開始前の初期状態です。　言い換えると、最初は①のように水を配置しておきます。

_{「金属すのこ」とは、上図のような板です。　水の移動は自由、物体は通過できない板状のものです。、これを、図１の①～⑥を通してある下限ストッパーとして使用します。}

上昇により、物体の底は押し上げられる。その分、「下限ストッパー＝金属すのこ」　と水槽底枠の間の水スペースは拡がります。　また、同時に、この水の増量と同じ分だけ、物体から上限ストッパーまでの水は減ります。（図１①～③、）

装置の説明（冒頭イラスト④、⑤、⑥）

上昇する物体の最上部（“三角帽子のテッペン”）は上限ストッパーにぶつかりつかり、そこで上昇は機械的に強制的に止まります　（④）。

この部分の詳細は下のようになっています。（図４）

 

もし上限ストッパーが無いと、物体は図１の①～③のように、喫水線まで上昇を続けます。しかし、物体の三角帽子のテッペンが上限ストッパーにぶつかると物体の上昇は強制的に止まります。　押し上げられた水は行き場を失い、上限ストッパーを突き破って装置は破壊されます。　この点の構造強度が担保されれば、三角帽子の下り斜面に沿って流れるしかない④。　結果、水は、三角形の底辺の両端に徐々に溜まり始めます⑤～⑥。そこは、多数の小穴が開いた「すのこ状」の板に繋がっています。　浴室のシャワーの噴出口のようなものです。　ただ、上限ストッパーとシャワー発生版の間のスペースが十分でないと上のプロセスは上手くいきません。

こうして、シャワー発生板が用意されます。

 

シャワーは重力で落下します。　シャワーは浮力には全く寄与しません。

（アルキメデスの原理は、連続的に密な流体が前提）

 図１④の時点で浮力を失うので、物体は重力による自由落下を開始します。ただし、落下したシャワーの水は下に溜まっていきます（図１④～⑤）。

 

その分と最初からある底の水スペースによって、浮力は回復していき下降速度は鈍っていきます。　どこかの時点で、シャワーの水は尽き果てて,物体は下限ストッパーでブロックされて止まります。　シャワーの水は止まり、物体は普通の水に包まれて、初期の①に戻り物体は上昇に転じます（図１①～③）。ちなみに、下限ストッパーの下の水量は①～⑥のどのステージにおいても不変、一定となります。　（変化する理由はありません）。

なお、初期状態の物体の底は、下限ストッパーより上でも良いのですが、上下往復運動のストロークを長くする目的で下限ストッパーに合わせました。

 産生エネルギーと電力

+物体は、①②③　の上下運動の繰り返し（図1）、この力学エネルギーを電気として取り出すことが最終目的です。　物体は、天井が一番高い位置（上限線）のときに止まり、また、物体の底が下限線に達しても止まります（図５）。

　一般に、形ある物体（剛体）の運動は、その物体の重心を代表にして行ないます。　つまり、重心という1点に、物体の全質量が集中して存在するというモデルを用いて解析を進めます。　

図１①～③の場合（上昇過程）　

物体が上限線でストップしたとき、物体が持つ位置エネルギー　U（ポテンシャル・エネルギー）は、下限線を基準にして、

 Ｕ＝Ｍｇｄ₌Ｗｄ　　Ｊ（　ジュール）　式３

 これは、図１の①→③の間に、浮力が行なった「仕事（物理量）」に相当します。

 電力にも関係する仕事率パワーとは、この力仕事を成し遂げた時間が関係します。　時間が短ければ短いほど大きなパワーとなります。　そこで、１サイクルに要す時間を調べます。

数値例１

この図８の例では、装置全体の高さは2 . 5m 程度。　上限線と下限線の間の距離 h を 2m　とします。

　　

物体の天井が上限線に達したとき物体がもつ位置エネルギーは、式３よりＵ＝Ｗｄ。これは浮力が１サイクルで行なった仕事量です。

パワー（仕事率）＝仕事量／時間なので、１サイクルにかかる時間を次に計算します。

 

重心間距離 ｄ を　1m とします（図６）。　重心間 1m の上昇時間は、式８より　t =    １．４４  秒。

次に、上限線から下限線までの水の落下時間は、、式９より　ｔ＝ 　   １．２６　秒。

以上より、１サイクルの時間T は

T ≈　（１．４４　＋　１．２６）　　／　２　＝１．３５　秒

しかし、実際には、水の抵抗や、水と物体の摩擦、落下水に働く空気抵抗があります。　これらの要因で　T　は上より若干長くなる筈です。　そこで　Ｔ ≈２．０　と概算します。

 

一方、重心の最高位置で物体が持つ位置エネルギーは、式３に於いて d=1なので　

Ｕ＝Ｍｇ x 1 =W　　式１０

Ｗは物体の重量。　浮力　Ｆ　は　Ｆ＝１．１Ｗ　（式７）　という縛りを安定性の理由で入れました。　

 

物体を50 x 50 x 50 cm³  =2500０ cm³の立方体＋三角帽子とすれば、アルキメデスの原理から、物体が排除した水の体積は　約２５　リットル、よって浮力は２５　kg 重　です。 物体の重量は概ね２５／１．１＝２２．７　kg　重となります。この重量調整は、物体を中空にして、６枚の壁の鋼材の厚さで調整します。

 さて、位置エネルギーは式１０よりＵ　＝２２．７　kg 重­

以上から、パワー＝U÷T ≈２２．７　／１．３５　Ｊ（ジュール）／秒　＝　１６．８ワット。１時間あたり、１６．８　 ３６００＝４．７　kワット時（kwh）　となります。

一方、平均的な４人家族の１日当たりの消費電力は下の資料によると１８．５khw です。　　このことは、本浮力発電装置を４時間程度の連続運転して蓄電すれば１日当たりの平均消費を賄えることになります。

数値例２

この例では、装置全体の高さは３０m 、断面積は６　x　６ = ３６　m²程度を想定します。　図９において、中の物体は２ x ２ x 2 =８　m³ の中空立方体。　排除する水の体積は８ｘ１００^３　cm³　＝８００００００　cm³=8０００リットル。　よって、その浮力Ｆは８０００ kg重　＝８トン、浮力は２５　kg 重　です。物体の重量は８／１．１＝７．３トンです。

重心間距離 ｄ を　１５m とします。　重心間 の上昇時間は、式８より

ｔ＝　30 / 0.1g　の平方根　 　５．５　秒

上限線から下限線までの距離 h を２０ｍとします。　すると物体の落下時間は、

ｔ　＝　40 / g の平方根　   ２．０　秒　

 

１サイクルに要す時間は式９より、概ね（５．５＋２．０）／　２　＝３．７５秒。　しかし、数値例１と同じ理由で、これより若干長めのT≈５　秒　と想定しておきます。

 

他方、物体重心位置が上限のときの位置ネルギーは　ｄ＝１５m, W=7.3トンであるから、U＝１０９．５　トン重＝１０９５００　kg(J)。

T≈５秒としてパワーは

P≈U／T　  ２．３ kワット

数値例１の約１５０倍となります。

物体の上下運動から発電について。

クランクシャフトの使用も考えられますが、

エネルギーのロスが少ないことが期待されるピストン運動直接発電が推奨できそうです。

ttps://pruning101.com/?p=1088　より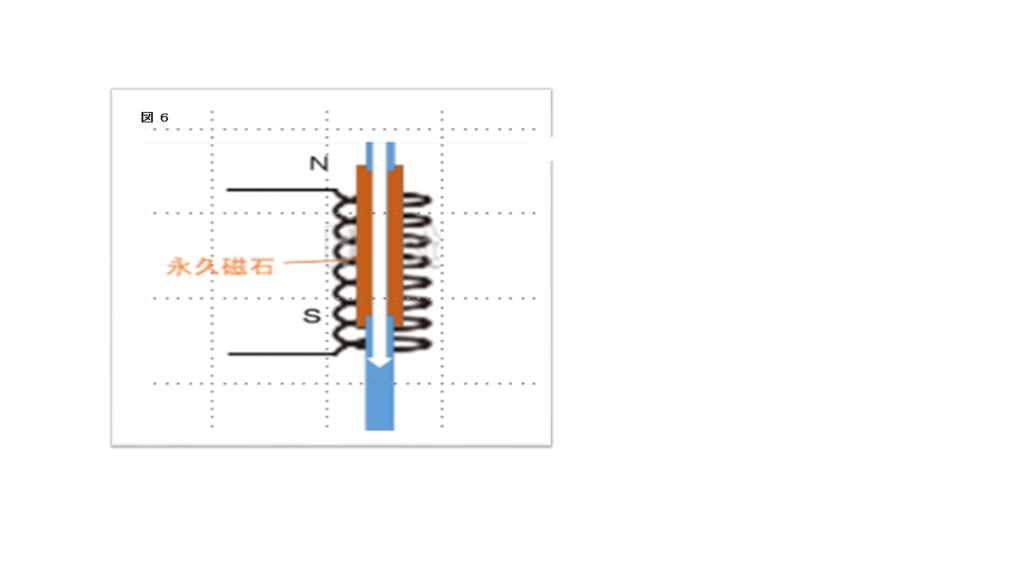

あとがき

従来の水力発電はダムなど高い所から水を落します。　

落ちた水は川となり最終的には海に放出されます。

そこから水蒸気が発生し雨雲を作ります。

そして、雨が降りダムに水が溜まります。

こうして、高↓低、　低↑高、　高↓低、　低↑高、・・・

という具合に水の無限循環が自然形成されます。

 

本ブログの発電では、低↑高　の部分を浮力が担います。元はと言えば、浮力は重力由来なので、１種の重力発電とも言えます。

 これは、、菅総理もバイデン新大統領も、気合をいれている脱炭素社会の方向性に合致していると思います。　目下、世界に類を見ない新しい発電方式となるように、内外特許の取得、プロットタイプの試作、検証実験の計画・準備をしています。