(改定)　浮力発電：ダブル水槽方式

 キーワード：　　アルキメデスの原理　ダブル水槽　（外水槽　と　内水槽）　電磁バルブ  浮力　　重力　喫水線

　

喫水線と船底を囲んだ体積に相当する水の重さが船の重さの指標のひとつ（排水量、排水トン）

 

本方式の浮力発電の特長はダブル水槽ですが、重要なのは内水槽の中にある「浮き箱」の上下方向の振る舞いです。

　アルキメデスの原理より、水中点線で囲んだ水の重さが浮力となります。

 

装置の基本構成

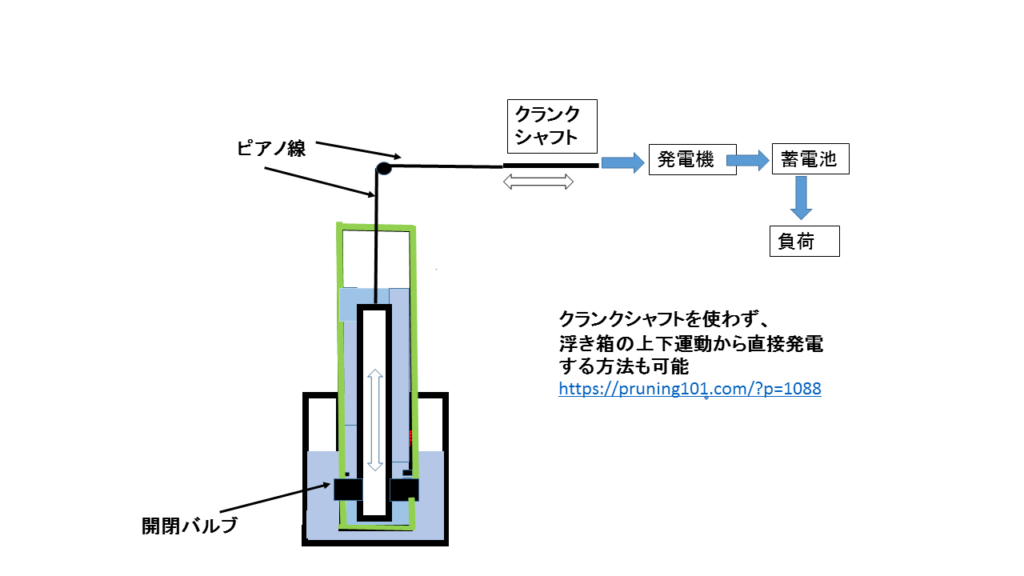
ダブル水槽方式では

内水槽と外水槽の水量の合計は常に一定。

内水槽に中に閉じ込められた「浮き箱」は上下方向に自由に移動が可能。

浮力（Ｂ）＞浮き箱の重さ（Ｗ、重力）のとき箱は上昇、Ｂ＜Ｗならば箱は沈下。

上は潜水艦の浮上、潜行に似ています。　内水槽はバラスト・タンクのような役目をします。

 

内水槽←→外水槽　の水の出し入れは、装置の底部に設置した1対の電磁バルブを介して次のように行う。

浮き箱の上端が喫水線を超えればバルブが開く。　下になるとバルブは閉じる。

ただし。バルブが閉のときでも、下限線の下で内水槽と外水槽の間は

水路で繋がっている。こうして内と外の水槽の合計量は不変に保たれる。

　

以上から図に示すように、

装置全体の振る舞いは周期的で①→・・・→⑥→①→・・・→⑥→・・・となります。　すなわち、

①浮力によって浮き箱は上に押し上げられる。

②　バルブが閉じる。　ただし、箱の周り（内水槽）に水が十分あるので、アルキメデスの原理により浮力は①とほぼ同じ。　（ただし、両水槽の合計水量一定の前提から外水槽の水位は若干下がる）

③　②が継続。　浮き箱は上昇を続け、やがて喫水線を越える。

④バルブが開く。　内水槽の水は一気に外水槽に吐きだされる。　浮力は激減、　

　浮き箱は自由落下のような状態。

⑤浮き箱は下限線に近づく。

①に戻る。　下限線を突破。　同時にバルブが開く。

• エネルギー源としての浮き箱と出力電力

 先ず、１サイクル（①・・・⑥）の間に「浮き箱」がした「仕事」を考えます。ここで仕事とは力学の言葉、浮き箱が創出したエネルギーのこと。

箱の上下運動はニュートンの法則によって、加速度をα [m/sec²  ]

とすれば、

しかし、今の場合、この積分を簡単に求めることは出来ません。

なぜならば、浮き箱の排水量、すなわち、浮力Bは時々刻々変わるからです。

 

そこで①②③の上昇過程と　③④⑤　の下降過程を分けて考えます。

 

上昇過程

浮力は①から徐々に増加、箱の重さと釣り合う喫水線で最大。この間、箱が十分に細長く浮き箱の先端が喫水線の高さを越えるとバルブが開く。この間、内水槽の水は常に大量にあり、上昇過程は重力に比べて浮力主導となる(B　>>　Ｗ)。この状況は、浮き箱の体積を大きくして実現できます。

内水槽の中で浮き箱が占める水の体積をＶ [ｍ^３]とします。　

浮き箱が排除する水の重さ、すなわち、浮力Ｂは水の比重＝１なのでＶｇ　となる。

上昇過程は浮力主導　Ｂ＞＞Ｗが前提だから、Ｂ＝Ｖｇと近似します。

 

すると、

式3に出てくる　Ｖｇ／Ｍg 　は重要なパラメータとなります。

Ｍ　は浮き箱の体積、Ｖg は浮き箱が占める水の重さ＝浮力、Ｍgは浮き箱の重量。つまり、Ｖｇ／Ｍg　は浮力が重力に比べてどの程度大きいかを指標です。

浮力が勝れば上昇時間は短くなる当然のことが式３で確認されます。

 

下降過程　④⑤

内水槽の水は大幅に減り、浮力は僅か。　浮き箱は自由落下と近似します。

上昇過程に比べて時間はかなり短くなることが予測できます。計算式は

加速度αはｇだからｔ＝(2h/g)　の平方根 となります。

 

• エナルギー源としての浮き箱と出力電力

 

 

先ず、１サイクル（①・・・⑥）の間に「浮き箱」がした「仕事」を考えます。ここで仕事とは力学の言葉、浮き箱が創出したエネルギーのこと。

箱の上下運動はニュートンの法則によって、加速度をα [m/sec²  ]

とすれば、

Mα _{=　 B  －  W}

ここでＭは箱の質量（kg）。　　

Wは箱の重さはW=M g（ｇは重力加速度定数 9.8m/sec²）。

 

 そこで、箱に働く加速度は

 　　α＝(Ｂ／Ｍ－1) ｇ

 となる。

 

次に、時間を考えます。　一般に加速度、時間(t),距離の関係は,ニュートンの法則から

(

しかし、今の場合、この積分を簡単に求めることは出来ません。

そこで①②③の上昇過程と　③④⑤　の下降過程を分けて考えます。

 

上昇過程

浮力は①から徐々に増加、箱の重さと釣り合う喫水線で最大。この間、箱が十分に細長く浮き箱の先端が喫水線の高さを越えるとバルブが開く。この間、内水槽の水は常に大量にあり、上昇過程は重力に比べて浮力主導となる(B　>>　Ｗ)。この状況は、浮き箱の体積を大きくして実現できます。

内水槽の中で浮き箱が占める水の体積をＶ [ｍ^３]とします。　

浮き箱が排除する水の重さ、すなわち、浮力Ｂは水の比重＝１なのでＶｇ　となる。

上昇過程は浮力主導　Ｂ＞＞Ｗが前提だから、Ｂ＝Ｖｇと近似します。

 

すると、　　　　　　　　　　　　　、

 

 

 

本装置の運転は昼夜を問わず可能ですから、２４時間連続運転すると

• ６２ x 24 =１．６２ x ２４ｘ６０ワット時=５．８kワット時

この数字は平均的な家庭(４人家族)が１日に消費する電力の約３０％にあたります。

（https://www.tainavi-switch.com/contents/1255/#ac_h2_index1　より）

 大きな電力を必要とする企業の工場などで採用する場合は、装置の身の丈（高さh）を増やすか（たとえば、３０～５０ｍ）、あるいは、１０本。２０本と複数設置します。

 

最後に、ここで書いた浮力発電は太陽光にも風力にも関係なく昼夜を問わず運用

できます。　また、燃料は不要、一定量の水さえあればＯＫです。