集団感染の数理モデルとシミュレーション（２）

基本的考えと前提

ここで、個体の「ウイルス量」とは何か？　次のような定義が考えられます。

（１）その人の体内に鼻や口から持ち込まれたウイルスの数

（２）体内を浮遊するウイルスの中で細胞に侵入してそこで定着した数。　この宿主細胞の中で増殖したウイルスも含みます。

（３）この内来ウイルスも①に含めます。

「うつし率」や「うつされ率」（pとq）は「率」だから1.0以下の数字です。

p =0.5　なら 50%　の感染効率です。

この率はウイルス量の定義と関係します。ここでは、結局、（２）も　（３）もひっくるめた（１）とします。

 

うつし率もうつされ率も、自分だろうと相手だろうと個体が違えば変わります。　体質、生活行動、免疫力、健康状態に

左右されます。　一般市民の集団感染の動態がテーマなので、pも qも個別に扱わず、

その集団一律に高低いろいろな数字を想定しながら考えます。

理論構築やコンピュータプログラムではpとq　に別の数値を与えるも対応可能です。

たとえば、一緒にみんなでジョッギング中、仲間との前後関係や風向きで、山中伸弥先生ご指摘のように、

人は同じでもpとqは大きく違います。　このシミュレーションも試したいところですが、

別の機会にして今回は全てp=qを仮定しました。

 

 

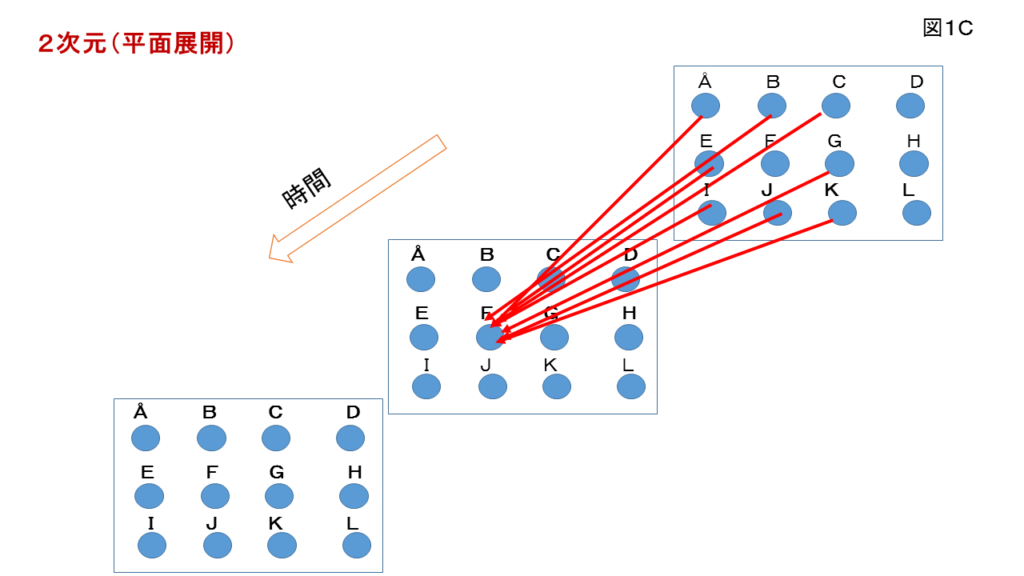
列状の１次元（図１Ｂ）集団で隣は前後または左右で二人です。　平面展開の二次元（図１Ｃ）ならば

隣は前後・左右・斜めと全部で８人の隣がいて、その分、集団感染のリスクは高くなると予想されます。

 

それと、時間的なシーケンスを考えることは重要です（図１Ｂ，Ｃ）。

ウイルス量の変化速度によって、現象的には時間の適切な単位は秒、分、時、日が考えられます。

一方、唾液検体ＰＣＲがいかに簡便、迅速になったとはいえ、対象個体から連続時間で

ウイルス量をモニターすることは今のところ現実的ではありません。

当局の発表も我々が得る情報も一日ごとの纏め集計です。

 

とはいえ、ここでは、シミュレーション対象の種類から、私が勝手に適切な「単位時間」を想像して

経過時間、経過日数などを割り振っています。

 

本ブログの後半では、平均的な普通の人々の集団に、一人の特殊な人物、すなわち、とんでもないウイルス量の持ち主

が外部から闖入（ちんにゅう）すると、その市民集団はどういうことになるかの予測をします。

なお、全てのシミュレション・データは感染して体内に取り込まれたウイルス量の推移予測に関する解析です。

新型コロナはＲＮＡウイルス、体の様々な部位に顕在的に悪さをするまでには、或る程度の時間経過が必要です。

この点、病気の発症状況については何も言えません。本ブログの対象外です。