PCRはウイルスの出入り口に於けるチェック検査に過ぎない（図１）。

しかも、陽性か陰性の２者択一（１か０）の単純なデータ）（図２）。体内ウイルスの増減が分るはずない。

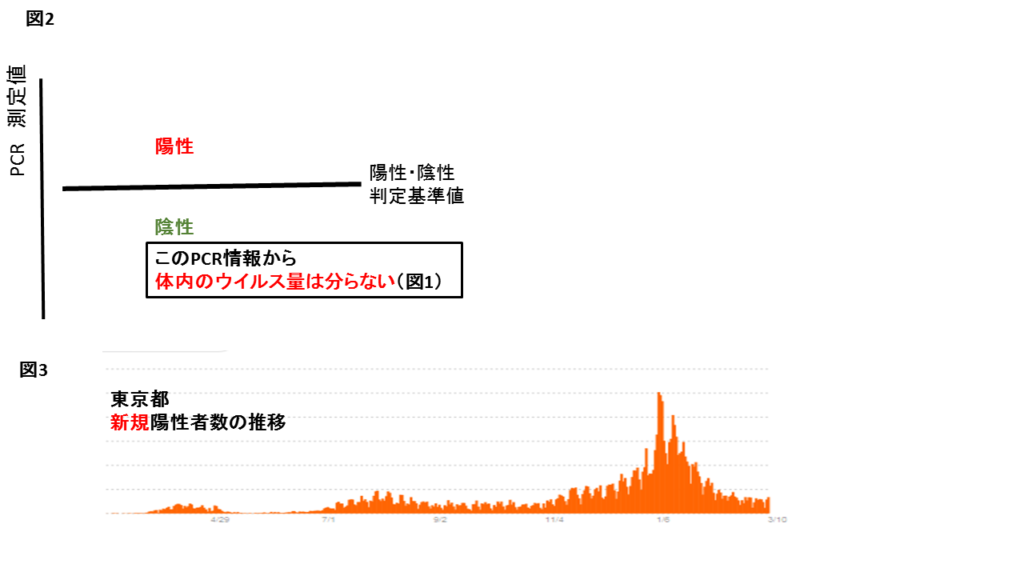
そのような陽性か陰性（１か０）の時系列が毎日公表される（例、図３）。

それを見て世間もメディアも一喜一憂。

しかし、図１からも明らかなように、肝心な点が分らない。体に入ったウイルスが人体細胞に侵入、着床後のウイルスはどうなった？　増殖中？　減少中？

また、たとえば、ＰＣＲ検査を「する抜ける」変異ウイルスが海外で見つかったという最近のニュース。

驚くことではない。　過去に侵入したウイルスが人体内で変異したのかもしれない。　ライバル株との競争に勝つため、あるいは、ワクチンを失効させるため。

一人歩きする新規陽性者数の時系列データ。（_{正確には新たに確認された陽性者数}）図３のような時系列データの深読みが求められる。

 

そもそも、新規陽性の判定は、PCR値が判定基準値を下から上へ跨ぐとき。　PCR新規陽性が多いということは、喩えると、入り口を通過して劇場に入った「入場者」（ウイルス）が数多く存在するということ、よって、普通に考えれば、劇場（体内）は大入り満員に近いと推察できる。

新規陽性者数の下げ止まりやリバウンドの科学的な説明は？

緊急事態宣言解除のタイミングをめぐって現在盛んに議論されている。

たとえば、東京都の場合、新規陽性者数が安定的に３００人以下、２００人以下、

いや、二桁にならないと駄目、と様々な数字を聞く。

どれも、過去の経験（第１波，２波）からの感覚的な印象意見のようで、

しっかりした科学的な根拠に乏しい感じ。　

この点、今回の「うつし率数理モデル」よる判断を提唱。

 

なお「うつし率」の定義と意味については、

市中感染の数理科学（１）

https://pruning101.com/?p=2079

の備考１を参照して下さい。

 

今は取りあえず、なぜ、下げ止まりやリバウンドが起こるか？　数式抜きの説明を以下で試みたいと思います。

たとえば、１万人の地域集団を考える。　新規感染者数が激減したが、５０人で下げ止まった。　９千５００人は行動自粛を励行したが（低いうつし率）、そうでない奴が５０人いたということです。この人達の体内ウイルス量は恐らく高い。　反省して自粛をキッチリ励行してPCR値を下げても、陽性→陰性の基準値が上から下に跨ぐケースとなり、それは新規陽性者としてカウントされない。よって、新規陽性者数の時系列に反映されない。　結果、下げ止まりとなる。

ではリバウンドについてはどうか　?　　気の緩みなどで、自粛を励行する人は大きく減るケースを想定します。　うつし率は上がり平均の体内ウイルス量は高くなる。

うつし率＝うつされ率とすれば貰う側のウイルス数も増える。相手（の体内ウイルス）が増える→自分も増える→相手も増える→自分も増える→・・・。　これは感染爆発に繋がる増悪のスパイラルです。

 

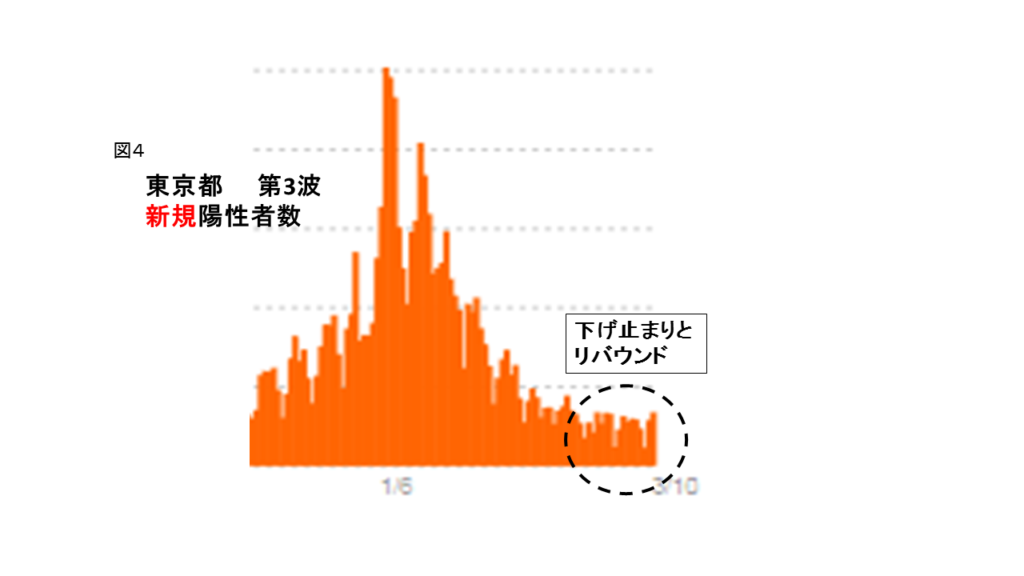
東京都の場合でも、下げ止まりから第４波に繋がるリバウンドの兆候が既に見える（図４）。

いくつかの自治体では下げ止まりからリバウンドの始まりがもっとハッキリ確認されているようです。

 

新規感染者数がゼロ付近に収まっている場合、どのような意味を持つのか？

二つの可能性があります。　

一つ目は、体内ウイルス量は高い数字でも、そこから減少が続いている場合。PCR値は上から下へと基準値を跨ぐので新規陽性になり得ない。

二つ目は、体内ウイルス量の増減は無く、一定のレベルを維持しているケース。　特に、このレベルの数字が高ければ危険なことは明白。

裏をかえせば、新規感染数の変化がゼロ付近で殆どなく沈黙しているときでも要警戒ということです。

 

以上は数理を使う必要がなく、また、実は新規感染データの深読みなどという大袈裟なものではなく、

図１から導かれる“自明の法則”と云えます。

 

うつし率モデルの運用　（１）検証

図４のような過去の新規感染者数の推移を再現できるか？

モデルの性質から、うつし率の時間的推移が正しく仮定されれば理論的に可能です。

しかし、うつし率は推定するしかない。

そこで、まずは、新規陽性の公表された時系列データを睨んでベストと思われるうつし率を、仮に、決めておく。

この際、前段落の「自明の法則」、および

市中感染の数理モデル（１）https://pruning101.com/?p=2079

の図２で得た経験値と勘が役立ちます。

たとえば、新規感染者の急上昇は高いうつし率、逆に、0人付近に収まったいるときは、低いうつし率の可能性（必ずしもそうでない）。

 

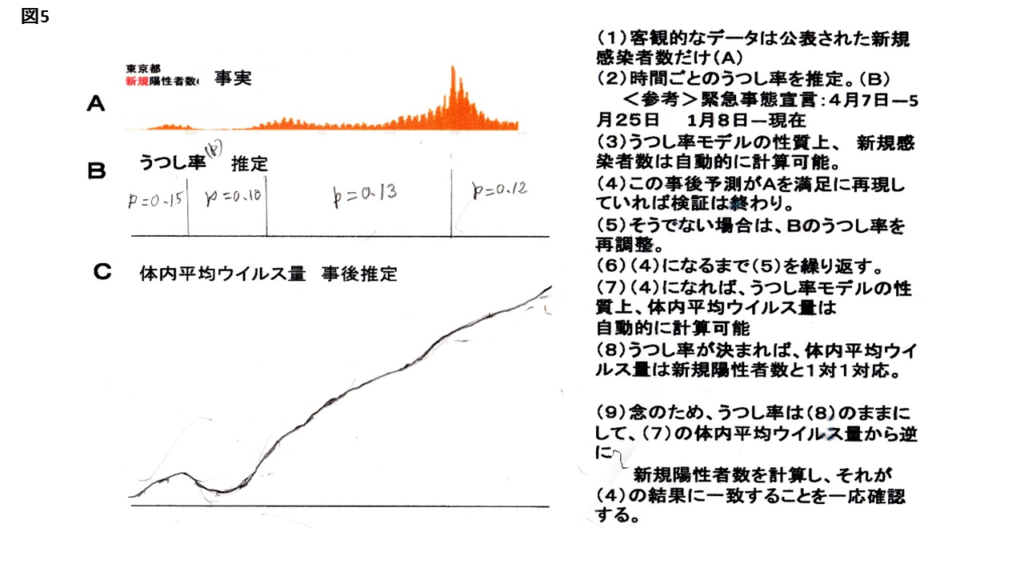
こして得た再現予測が概ね満足できるものならば、体内ウイルス量（平均）の図５Bのように推定が出来ます。

その上で、暫定うつし率はそのままにして、推定・体内量から逆に推定・新規感染者数を計算する。

この結果が、実際の新規感染者数の時系列データ（例：図３）と概ね一致すれば、うつし率モデルは一応完結です。

そうでない場合はうつし率を再調整します。

 

検証の対象を東京都にします（図３）。

図３の細部までの検証ではなく、グラフの山や谷のタイミングのトレンドが実際と一致することが目標です。

しかし1千万人を超える都民全員をモデルに乗せることは、スーパーコンピュータでも現実的ではない。

ここで助けとなるのが、大数の法則です。

大数の法則（Ｌａｗ　ｏｆ　ｌａｒｇｅ　ｎｕｍｂｅｒｓ）とは

https://mba.globis.ac.jp/about_mba/glossary/detail-12377.html

サンプル数が十分に多ければ、全体（母集団）の真実を反映するというものです。

たとえば、市長選挙、開票投票が１０人や２０人では何も言えない。しかし、投票締め切りから数分後にメディアが「当選確実」と報道することは珍しくありません。疫学調査、マーケッティング調査、世論調査アンケートでも大数の法則が用いられる。

ここでは対象都民を１万人としました。　市中感染の数理モデル（１）https://pruning101.com/?p=2079でも対象は1万人。　数字を3万人、５万人と増やしても結果のトレンドは同じだったことは指摘済みです。

とはいえ、1年３６５日の時系列結果を求めることは大変で特別な工夫をしました（次回で詳細）。

ところが、１０日前、使用中のｕｎｉｘ系ＯＳ（リナックス）を搭載したパソコンが突然ダウン。

電源部がやられました。　換気がよくない部屋で保証期間がとっくに過ぎた古いＰＣを、一日２４時間毎日で毎日連続運転

した結果と推察。

今から数日内に修理が終る見通しです。　手書きの汚い図5Ｂの体裁は違うものに代えます。

 

このことは、次の「うつし率モデルの運用　（２）予測」の手書きの図６についても同様です。

うつし率モデルの運用　（２）予測

 

現在の数値を初期値として、以後のうつし率の推移を様々に想定します。

これらの、それぞれについて、新規感染者と体内ウイルス量の将来の動向をうつし率モデルを使って計算します。

ＰＣの修理が完了するまでの、とりあえずの見通しが図６です。

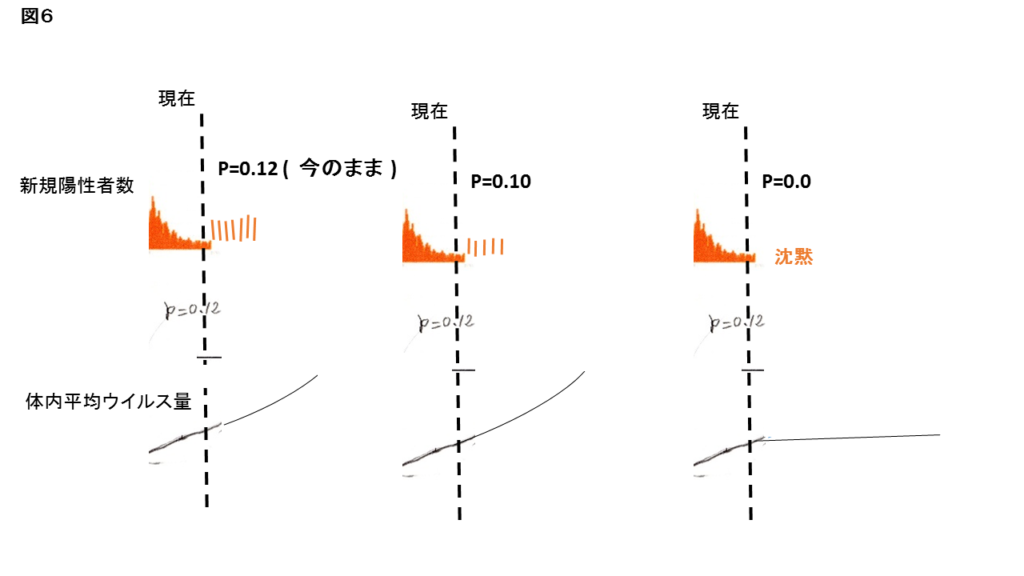
行動規制の段階的緩和（緩和の小出し）は効果があるか？

市中感染の数理科学（３）https://pruning101.com/?p=2134を振り返ると、小出しは、そのタイミングを慎重にしないと私は懐疑的です。

他に気になるのは、うつし率が０のケース。　これは全員がそれぞれ誰にも接触しない「個人別鎖国」。

集団免疫は起り得ません。

 

ウイルスの出入りが全くないので、体内で何も起らなければ体内ウイルスの量は不変です。

あとは、各人の「自力免疫」たとえば、リンパ球のひとつＢ細胞の活性化、igg抗体の産生がある。

ワクチンによる中和抗体もあるが、今回の「市中感染の科学」の全体も、その「うつし率モデル」もワクチンは考慮していません。　また、　医療態勢の状況も全く考慮していません。　ちなみに、今日の医療の逼迫を新規陽性者数のグラフと結びつけて世間は憂慮する印象があります。　個人的には、医療態勢の逼迫は、むしろ、　重症者や死者の増加に反映されているのではないか、と思っています。

あと、感染力が高いとされる変異ウイルスの存在も今回の「市中感染の科学」では想定していません。

憂慮されるこの問題については、後日別途に扱う予定です。　昨年７月のブログ

https://pruning101.com/?p=1535

と似たような結果が得られるのではないかと予想しています。

、